Clarke 变换
克拉克变换(Clarke Transform)是一种将三相交流电系统的电压或电流从三相坐标系(ABC坐标系)变换到两相静止坐标系$\alpha\beta$ 坐标系)的数学变换。它广泛应用于电机控制和电力电子领域,以简化控制算法。
克拉克变换实际上就是降维解耦的过程,把难以辨明和控制的三相相位差 $120^\circ$ 电机波形降维为二维矢量。从此复杂的三相变化问题就降解为了 $\alpha-\beta$ 坐标轴的数值变化问题。
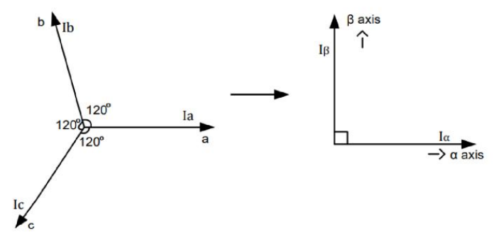
Clarke 变换的公式推导
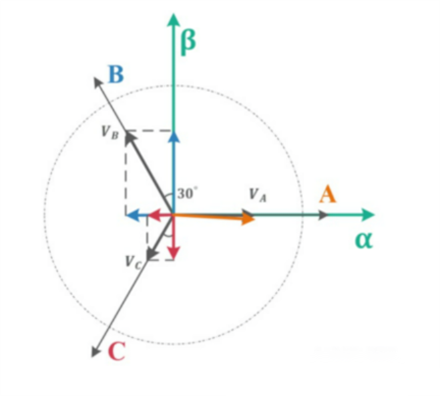
设 $V_a$、$V_b$、$V_c$ 是三相电压,三相系统中的相位角分别为:
- $V_a$ 的相位角为 $0^\circ$
- $V_b$ 的相位角为 $120^\circ$
- $V_c$ 的相位角为 $240^\circ$
我们希望将这三相系统转换到 $\alpha$-$\beta$-$0$ 坐标系。
1. 定义 $\alpha$-$\beta$ 坐标系
在 $\alpha$-$\beta$ 坐标系中,电压向量可以表示为:
\[\mathbf{V}_\alpha = V_a - V_b \cdot \sin(120^\circ) - V_c \cdot \cos(240^\circ)\] \[\mathbf{V}_\beta = V_b \cdot \cos(120^\circ) - V_c \cdot \sin(120^\circ)\]将这些值代入 $\alpha$ 和 $\beta$ 分量的表达式中,我们得到:
2. 计算 $\alpha$-$\beta$ 坐标中的电压
$\alpha$ 分量:
\[V_\alpha = V_a + V_b \cdot \left(-\frac{1}{2}\right) + V_c \cdot \left(-\frac{1}{2}\right)\] \[V_\alpha = V_a - \frac{1}{2} \cdot (V_b + V_c)\]$\beta$ 分量:
\[V_\beta = V_b \cdot \frac{\sqrt{3}}{2} + V_c \cdot \left(-\frac{\sqrt{3}}{2}\right)\] \[V_\beta = \frac{\sqrt{3}}{2} \cdot (V_b - V_c)\]3. 引入标量因子
为了保证变换的功率不变,通常在变换矩阵中引入一个标量因子:
\[\begin{bmatrix} V_\alpha \\ V_\beta \end{bmatrix} = \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \cdot \begin{bmatrix} V_a \\ V_b \\ V_c \end{bmatrix}\]\[\begin{bmatrix} V_\alpha \\ V_\beta \end{bmatrix} = \sqrt{\frac{2}{3}} \cdot \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \cdot \begin{bmatrix} V_a \\ V_b \\ V_c \end{bmatrix}\]等功率变换,所以标量因子为 $\sqrt{\frac{2}{3}}$
\[\begin{bmatrix} V_\alpha \\ V_\beta \end{bmatrix} = \frac{2}{3} \cdot \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \cdot \begin{bmatrix} V_a \\ V_b \\ V_c \end{bmatrix}\]等幅值变换,所以标量因子为 $\frac{2}{3}$
4. 零序分量
\[V_0 = \frac{1}{\sqrt{3}} \cdot (V_a + V_b + V_c)\]零序分量 $V_0$ 定义为三相电压之和的平均值:
通过 Clarke 变换,三相电压 $V_a$、$V_b$、$V_c$ 被转换到 $\alpha-\beta-0$ 坐标系中,这样的表达形式可以直接应用于各种电力电子系统中。
等幅值 Clarke 变换
等幅值 Clarke 变换(Equal Magnitude Clarke Transform)是一种特殊形式的 Clarke 变换,旨在保持原始三相系统和变换后的双相$\alpha-\beta$系统的幅值一致。这种变换的目标是使得在 $\alpha-\beta$ 坐标系中得到的电压或电流分量的幅值与原始三相系统中的幅值相等,从而更直观地反映系统的物理量。
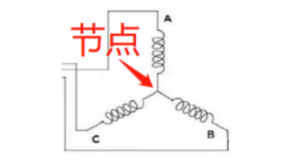
基尔霍夫电流定律(Kirchhoff’s Current Law, KCL)表示,对于一个电路中的任何节点,进入节点的电流之和等于离开节点的电流之和。这个定律反映了电荷守恒。
-
三相系统中的电流分布
\[I_a + I_b + I_c = 0\]
在一个平衡的三相系统中,假设三个相电流为 $I_a$、$I_b$ 和 $I_c$。根据基尔霍夫电流定律,对于三相系统的中性点,进入中性点的电流和离开中性点的电流之和为零: -
等幅值 Clarke 变换的矩阵形式
\[\begin{bmatrix} I_\alpha \\ I_\beta \end{bmatrix} = \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \cdot \begin{bmatrix} I_a \\ I_b \\ I_c \end{bmatrix}\]
通过 Clarke 变换,将三相电流 $I_a$、$I_b$ 和 $I_c$ 变换为 $\alpha$-$\beta$ 坐标系中的电流 $I_\alpha$ 和 $I_\beta$: -
KCL 在 Clarke 变换中的应用
在变换过程中,基尔霍夫电流定律仍然适用。变换后的 $\alpha$-$\beta$ 坐标系中的电流 $I_\alpha$ 和 $I_\beta$ 仍然满足基尔霍夫电流定律。由于 $\alpha$ 和 $\beta$ 轴是相互正交的,任何进入 $\alpha$-$\beta$ 系统节点的电流的合成依旧保持平衡。 - 功率守恒
通过等幅值 Clarke 变换,三相系统中的瞬时功率在 $\alpha$-$\beta$ 坐标系中得到保留。这可以理解为基尔霍夫电流定律在另一个坐标系下的体现,即变换前后电流的相互关系依旧遵循电荷守恒原则。 - 等幅值 Clarke 变换的化简
由等幅值
\[I_\beta = {\frac{2}{3}} \cdot \left( {\frac{\sqrt 3}{2}} \cdot I_b - \frac{\sqrt 3}{2} \cdot I_c \right)\] \[= \frac{\sqrt 3}{3} \cdot \left( I_b - I_c \right)\] \[= \frac{1}{\sqrt 3} \cdot \left( I_b - I_c \right)\]得
\[I_\beta = \frac{1}{\sqrt 3} \cdot \left( I_b - I_c \right)\] \[=\frac{1}{\sqrt{3}} \cdot \left( I_b +I_a + I_b \right)\] \[=\frac{1}{\sqrt{3}} \cdot \left( I_a + 2I_b \right)\]推出
\[I_\alpha = I_a\] \[I_\beta = \frac{1}{\sqrt{3}} \cdot \left( I_a + 2I_b\right)\]最终得到
Clarke 逆变换
\[I_a = I_\alpha\]由
\[I_\beta = \frac{1}{\sqrt{3}} \cdot \left( I_a + 2I_b \right)\] \[I_\beta = \frac{1}{\sqrt{3}} \cdot \left( I_\alpha + 2I_b \right)\] \[\sqrt{3} \cdot I_\beta = I_\alpha + 2I_b\] \[2I_b = \sqrt{3} \cdot I_\beta - I_\alpha\]带入得
\[I_b = \frac{1}{2} \cdot \left( \sqrt{3} \cdot I_\beta - I_\alpha \right)\]推出
\[I_c = -I_a - I_b\]同理由
\[= -I_\alpha - \frac{1}{2} \cdot \left( \sqrt{3} \cdot I_\beta - I_\alpha \right)\] \[= \frac{1}{2} \cdot \left( -2I_\alpha - \sqrt{3} \cdot I_\beta + I_\alpha \right)\] \[= \frac{1}{2} \cdot \left( -I_\alpha - \sqrt{3} \cdot I_\beta \right)\]带入得
最终得到
\[I_a = I_\alpha\] \[I_b = \frac{1}{2} \cdot \left( \sqrt{3} \cdot I_\beta - I_\alpha \right)\] \[I_c = \frac{1}{2} \cdot \left( -I_\alpha - \sqrt{3} \cdot I_\beta \right)\]