1、Park变换
将静止坐标系α-β变换到同步旋转坐标系d-q的坐标变换称为Park变换。是目前分析同步电动机运行最常用的一种坐标变换,由美国工程师派克(R.H.Park)在1929年提出。派克变换将定子的a,b,c三相电流投影到随着转子旋转的直轴(d轴),交轴(q轴)与垂直于dq平面的零轴(0轴)上去,从而实现了对定子电感矩阵的对角化,对同步电动机的运行分析起到了简化作用。
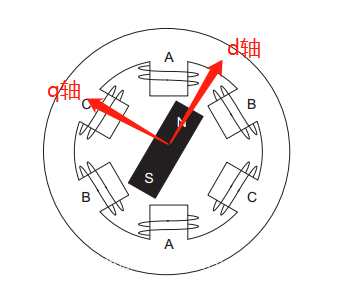
𝑑𝑞坐标系相对与定子来说是旋转的坐标系,转速的角速度和转子旋转的角速度相同,所以,相当于转子来说,𝑑𝑞坐标系就是静止的坐标系;而𝑖𝑑和𝑖𝑞则是恒定不变的两个值,具体如下图所示:
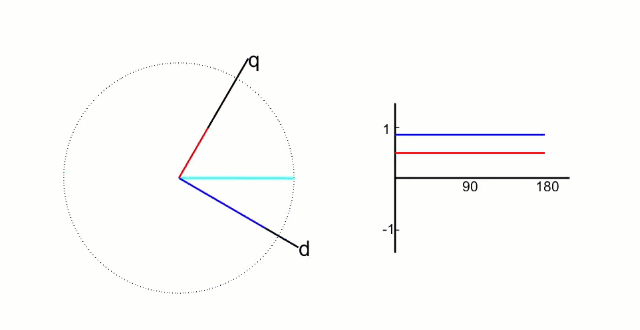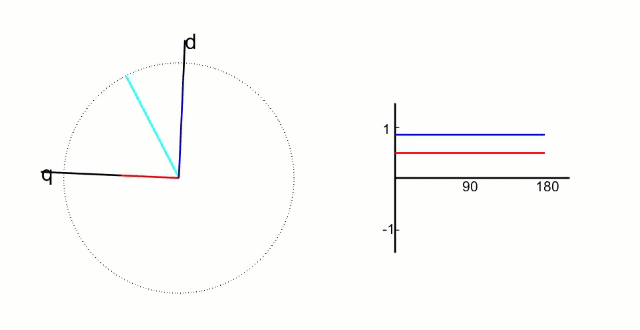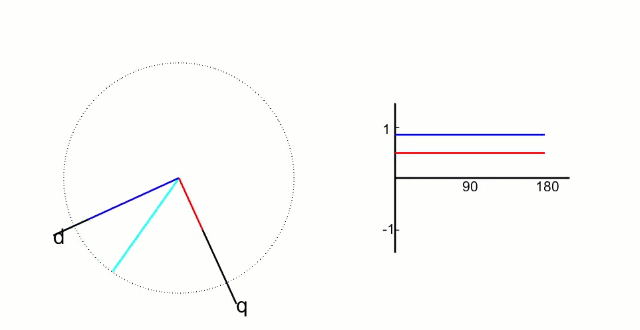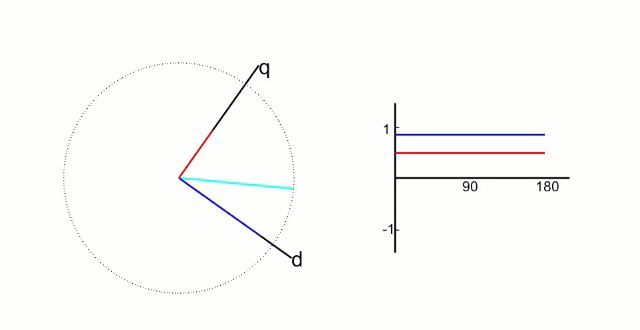
根据物理结构,我们发现:
𝑑 轴方向与转子磁链方向重合,又叫直轴:
𝑞 轴方向与转子磁链方向垂直,又叫交轴:
𝑑轴和𝑞轴如下图所示:
2、Park变换计算过程
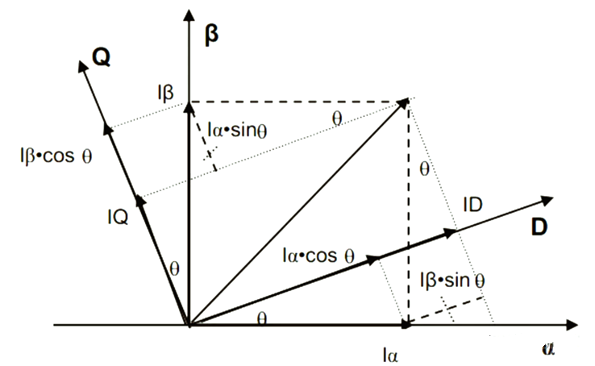
\[I_D = I_αcosθ + I_βsinθ\] \[I_Q = I_βcosθ - I_αsinθ\]如上图所示,d-q坐标系与α-β坐标系直接夹角θ,就是电角度,此θ是随转子转动的,应该注意的是,Park变换和后面讲的反Park变换中所需要传入的角度θ都是电角度而非转子的机械角度。接下来开始进行数学的分析: 我们把α和β轴上的 $I_α$ ,$I_β$通过正交分解,分解到d-q坐标轴上去,$I_α$在d轴上的分量 = $I_αcosθ$,$I_β$在d轴上的分量 = $I_βsinθ$,$I_α$在q轴上的分量 = -$I_αsinθ$,$I_β$在d轴上的分量 = $I_βcosθ$,综上可以得到如下结果:
\[\begin{bmatrix} I_D \\ I_Q \end{bmatrix} = \begin{bmatrix} cosθ & sinθ \\ -sinθ & cosθ \end{bmatrix} \begin{bmatrix} I_α \\ I_β \end{bmatrix}\]写成矩阵形式
\[\begin{bmatrix} I_D \\ I_Q \end{bmatrix} = \begin{bmatrix} cosθ & sinθ \\ -sinθ & cosθ \end{bmatrix}^{-1} \begin{bmatrix} I_α \\ I_β \end{bmatrix}\]对矩阵取逆
\[\begin{bmatrix} I_α \\ I_β \end{bmatrix} = \begin{bmatrix} cosθ & -sinθ \\ sinθ & cosθ \end{bmatrix} \begin{bmatrix} I_D \\ I_Q \end{bmatrix}\]得到 park逆变换