SVPWM介绍
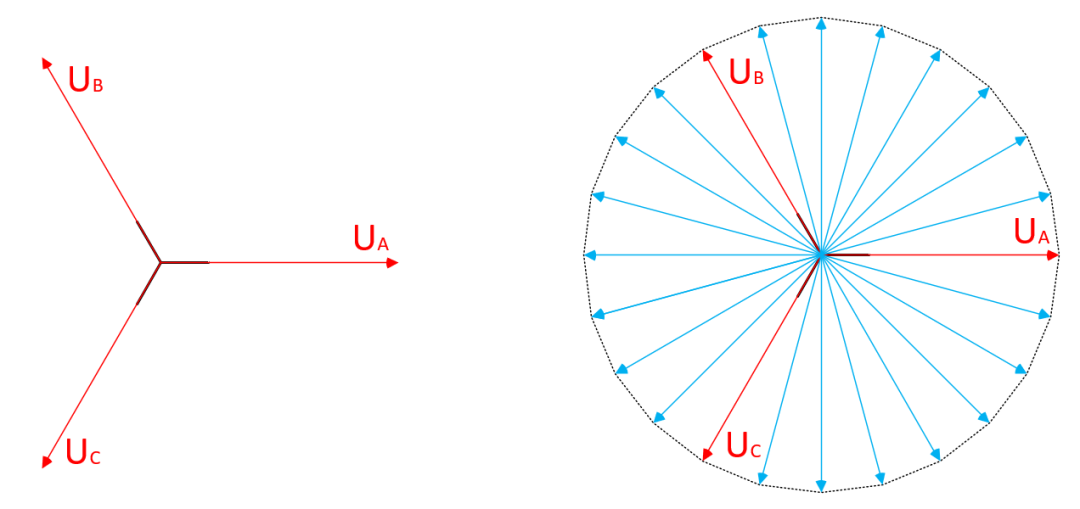
SVPWM(Space Vector Pulse Width Modulation),即空间矢量脉宽调制。SVPWM的理论基础是平均值等效原理,即在一个开关周期Ts内,对基本矢量电压加以组合,使其平均值与给定电压矢量相等。通过控制基本矢量电压的作用时间,使合成的目标矢量电压在空间位置按照接近圆形轨迹旋转,所产生的实际磁通去逼近一个理想的磁通圆。模型如下图所示,采样点数越多,就越逼近理想磁通圆,理论上采样点数无穷多时就是理想磁通圆了。
SVPWM 实现方法
1. Clarke 变换 (abc to αβ)
将三相静止坐标系中的三相电压 ( u_a ), ( u_b ), ( u_c ) 转换到 α-β 静止坐标系:
\[u_\alpha = u_d \cdot cosθ - u_q \cdot sinθ\] \[u_\beta = u_q \cdot cosθ + u_d \cdot sinθ\]2. 计算三个基矢量 $u_1$, $u_2$, $u_3$
在 α-β 平面中,计算三个基矢量 $u_1$, $u_2$, $u_3$,它们对应三个不同的相电压:
\[u_1 = u_\beta\] \[u_2 = -\frac{\sqrt{3}}{2} \cdot u_\alpha - 0.5 \cdot u_\beta\] \[u_3 = \frac{\sqrt{3}}{2} \cdot u_\alpha - 0.5 \cdot u_\beta\]3. 确定扇区
根据 $u_1$, $u_2$, $u_3$ 的符号,确定当前电压矢量所在的扇区:
\[\text{sector} = (u_1 > 0) + 2 \cdot (u_2 > 0) + 4 \cdot (u_3 > 0)\]4. 根据扇区选择作用时间 $t_1$, $t_2$ 和零矢量时间 $t_0$
-
扇区 1:
\[t_1 = u_3\] \[t_2 = u_1\] -
扇区 2:
\[t_1 = -u_1\] \[t_2 = -u_3\] -
扇区 3:
\[t_1 = u_1\] \[t_2 = u_2\] -
扇区 4:
\[t_1 = -u_2\] \[t_2 = -u_1\] -
扇区 5:
\[t_1 = u_3\] \[t_2 = u_1\] -
扇区 6:
\[t_1 = u_2\] \[t_2 = u_3\]
5. 归一化和零矢量时间 $t_0$ 计算
计算矢量作用时间的归一化系数 $k_{\text{svpwm}}$ 和零矢量时间 $t_0$:
\[\text{sum} = t_1 + t_2\] \[k_{\text{svpwm}} = \begin{cases} \frac{T_s}{\text{sum}} & \text{if } \text{sum} > T_s \\ 1 & \text{if } \text{sum} \leq T_s \end{cases}\] \[t_1 = t_1 \times k_{\text{svpwm}}\] \[t_2 = t_2 \times k_{\text{svpwm}}\]计算零矢量时间 $t_0$:
\[t_0 = \frac{T_s - t_1 - t_2}{2}\]6. 计算最终的 PWM 时间 $t_a$, $t_b$, $t_c$
根据不同的扇区,计算 PWM 输出时间:
-
扇区 1:
\[t_a = t_1 + t_2 + t_0\] \[t_b = t_2 + t_0\] \[t_c = t_0\] -
扇区 2:
\[t_a = t_0\] \[t_b = t_2 + t_0\] \[t_c = t_1 + t_2 + t_0\] -
扇区 3:
\[t_a = t_0\] \[t_b = t_1 + t_2 + t_0\] \[t_c = t_2 + t_0\] -
扇区 4:
\[t_a = t_2 + t_0\] \[t_b = t_1 + t_2 + t_0\] \[t_c = t_0\] -
扇区 5:
\[t_a = t_1 + t_2 + t_0\] \[t_b = t_0\] \[t_c = t_2 + t_0\] -
扇区 6:
\[t_a = t_2 + t_0\] \[t_b = t_0\] \[t_c = t_1 + t_2 + t_0\]